Everyone loves $\pi$. It’s usually the first irrational number someone encounters. $\pi$ is conceptually simple enough that it can be explained with basic geometry.
$\pi$ is the ratio between the circumference and the diameter. Usually, written as:
$$ C = 2\pi r $$
where $C$ is the circumference, $r$ is the radius (half of the diameter) and $\pi$ is famously $3.14159..$.
But why does $\pi$ have to have that value? Could it have some other value? The answer is yes! But to figure that out, we first have to talk about circles which are closely tied to the definition of $\pi$.
Circle
Since the definition of $\pi$ depends on two properties of a circle (circumference, radius), it’s good to figure out what a circle even is. Mathematically, a circle is the collection of all points that are an equal distance from the center. So if the radius of a circle is 1, then the circle is the collection of all the points that are 1 unit distance away from the center.
In practical terms, a circle tells you all the points that have an equal “cost”. For example:
- If you start running from the center, then the circle represents all the farthest points you can reach in a given amount of time. Here the distance is measured in units of time.
- If you start driving from the center, then the circle represents all the farthest points you can reach in a given amount of fuel. Here the distance is measured in units of fuel.
But not all constant-cost functions will create the same shape. For example, suppose you are sailing on a windy day. Traveling in the direction of the wind will be easy but traveling orthogonal to the wind will require more effort and traveling against the wind will require significant effort. So for fixed effort, the farthest points you can travel will create an ellipse shifted against the direction of the wind.
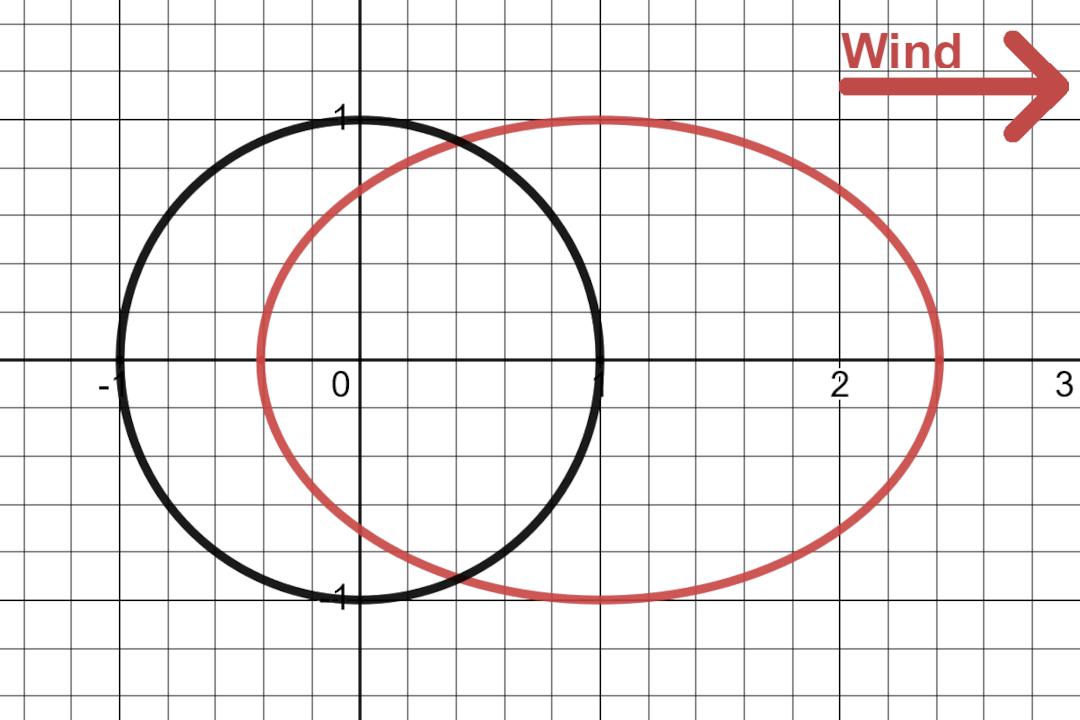
But does this cost-function (effort needed to sail) define a proper distance? Can we use it to measure radius and measure circumference? Seems kinda arbitrary to say yes or no. If time and fuel can all be “distances” in some situations then why couldn’t effort be a distance in this situation? Fortunately, we don’t have to make an arbitrary decision here since we can rely on a preexisting concept that defines what kinds of cost functions are valid distances.
Metrics
Mathematics can be seen as a logic game. You start with a set of assumptions and you come up with all the logical conclusions you can from that. Then, if someone else finds a situation that fits those assumptions, they can benefit from the pre-discovered logical conclusions. This means that if some conclusions require fewer assumptions, then those conclusions are more generally applicable.
As a result, mathematics goes through continuous cycles where mathematicians go back and trim down the assumptions needed for any mathematical system. For example, a lot of geometry from the times of the Greeks used only the single definition of distance: the Euclidean distance ($d = \sqrt{x^2 + y^2}$). We even named it after the Greek mathematician. Even Newton relied solely on Euclidean distance when he invented Calculus. Then, in the early 20th century, mathematicians realized that any function can be used as a distance function, as long as it followed some basic requirements. As long as the distance function followed those requirements, a lot of the established math would still work. So you could still do geometry and calculus and topology with just minor tweaks. Functions that fit these requirements are called metrics.
A function is a metric if it follows the following rules:
- The distance between a point and itself is always 0. If you don’t go anywhere, the distance traveled is 0.
- The distance between any two different points is always positive
- The distance from $a$ to $b$ is the same as the distance from $b$ to $a$
- Going directly from $a$ to $c$ is at least as fast as going from $a$ to $b$ and then from $b$ to $c$
Now, with these requirements, does “effort to sail” define a metric? The answer is no. We can probably debate 1 and 2 but 3 is very clearly not true. If $b$ is downwind of $a$, then the effort in one direction is smaller than the effort in the opposite direction.
Okay, so what functions are a metric? There are two classic examples: Manhattan distance and maximum distance.
Manhattan Distance
When you are driving in a city grid, you can’t drive diagonally. You have to drive in one grid direction and then the other. When you drive like this, the distance between two points is just $d = x + y$. This is popularly called the Manhattan distance or the taxicab distance.
One application of this metric is measuring accuracy. Suppose you are asked to predict the total population change of two cities. If you guess within 1,000 people, then you win a prize. You can visualize this by charting the population change of one city on the x-axis and the population change of the other city on the y-axis. Then a “circle” around your guess with a radius of 1,000 tells you the range where you can still win the prize.
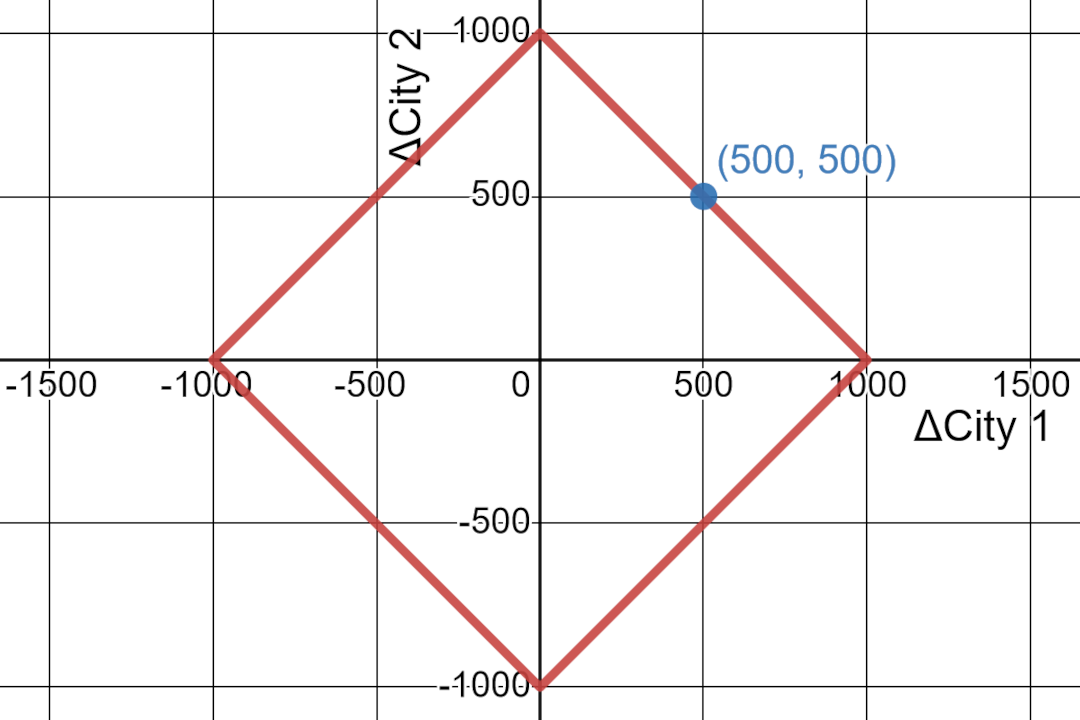
The circle looks like a rotated square!
The circle has radius of 1,000 but what is its circumference? If we use the Manhattan distance to measure the circumference then each line has a distance of 2,000 ($x + y = 1000 + 1000$) and since there are 4 lines, the circumference is 8,000. This means:
$$ C = 2 \pi r $$ $$ 8,000 = 2 \pi (1,000)$$ $$ 4 = \pi $$
In the universe where you measure distance using the Manhattan distance, the value of $\pi$ is 4!
Maximal Distance
Another distance function that is a valid metric is the maximal distance: $d = max(x,y)$. So instead of combining x and y, we use the larger of the two as the distance.
A lot of times when you are doing multiple things at the same time, it only matters how long the longest item takes. For example, suppose you need to prepare two ingredients for a dish, and you can prepare the ingredients in parallel. The amount of time you need to finish your dish is as long as the slowest ingredient.
Suppose for a cooking competition, you are required to finish cooking in exactly 60 minutes plus/minus 5 minutes. Then how much time can each ingredient take? If we use the x-axis to represent the time ingredient 1 takes and the y-axis to represent the time ingredient 2 takes, then we can draw a 5 minutes-wide circle that tells us how long each ingredient can take.
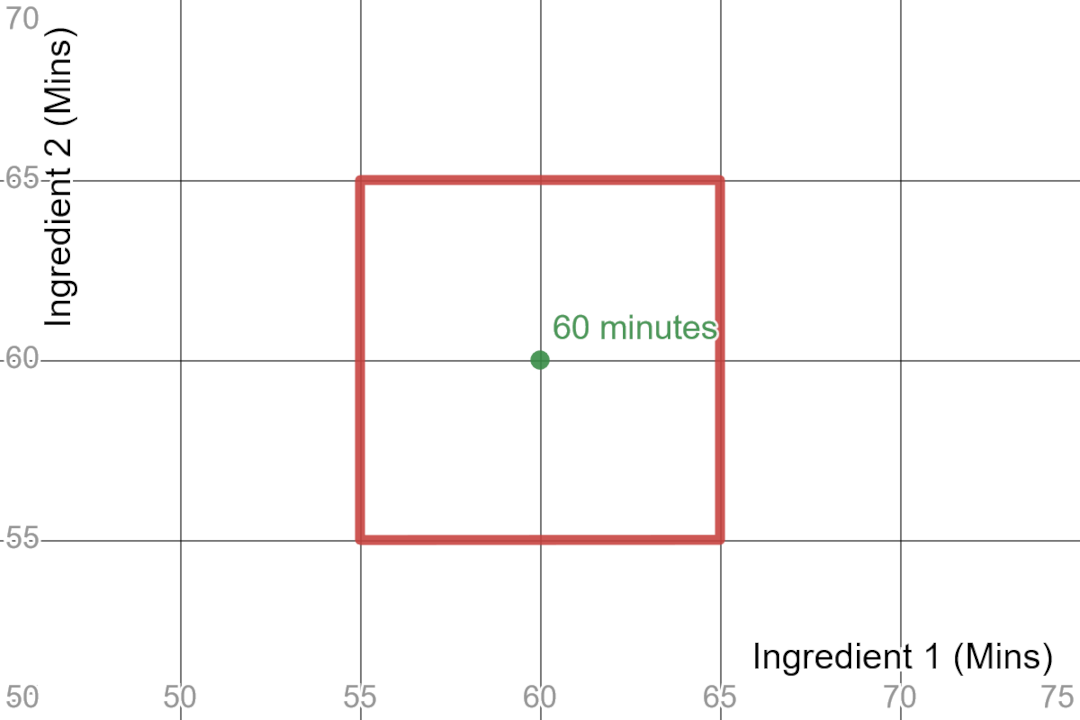
This circle looks like a regular square! The circle has radius 5 but what is its circumference? Each line has a distance of 10 and there are 4 lines so the circumference is 40.
$$ C = 2 \pi r $$ $$ 40 = 2 \pi 5 $$ $$ 4 = \pi $$
And again, in the universe where distance is measured using the maximal distance, the value of $\pi$ is 4!
p-norm
Till now we have covered three distances: Euclidean, Manhattan, and Maximal. What other examples can we look at? Well, we have the p-norm metric which is a collection of infinite metrics defined as:
$$ d = \left(x^p + y^p\right)^{1/p}$$
where $p$ can be any number greater than or equal to 1.
The cool thing about p-norms are that they are a generalization of the metrics we covered before. Euclidean, Manhattan, and maximal distances are specific examples of p-norms. When $p$ is 1, we have the Manhattan distance. When $p$ is 2, we have the Euclidean distance. When $p$ is $\infty$, we have the maximal distance. So Manhattan distance and maximal distance are the extremes of the p-norms.
Here are what circles look like in different p-norms:
Just as we did before, the circumference and the value of $\pi$ can be calculated for the different p-norms. In previous examples, we were able to calculate the circumference just by looking at it, since they were straight lines but that strategy doesn’t work in general. So, for the rest of the shapes we need to caculate the circumferences computationally. We can write a program to tell a computer to walk around the circle and track the distance traveled. Fortunately, someone else has already done this work so we can refer to their results1.
| p | $\pi$ |
|---|---|
| 1 | 4 |
| 1.1 | 3.757… |
| 2 | 3.141… |
| 2.25 | 3.155… |
| 3 | 3.259… |
| 11 | 3.757… |
| $\infty$ | 4 |
In addition to calculating these values, the paper linked above also proves that 3.14159 is the smallest value of $\pi$ possible for all the p-norms. Our regular $\pi$ is the smallest possible $\pi$ in the family of p-norms!
All Metrics
While there are infinitely many p-norm metrics, there are infinitely more metrics that are not p-norms. What are the values of $\pi$ in all the other metrics?
This article by Sahoo proves that $\pi$ is between 3 and 4 for all metrics. We have seen the metrics that give us $\pi = 4$. What’s the metric that gives us $\pi = 3$?
The answer is a little gnarly2
$$ d = \frac{1}{2\sqrt{3}}\sum_{n=1}^6\left|x\sin\left(\frac{\pi n}{3}\right)+y\cos\left(\frac{\pi n}{3}\right)\right| $$
But drawing out the circle for this metric gives us a hexagon.
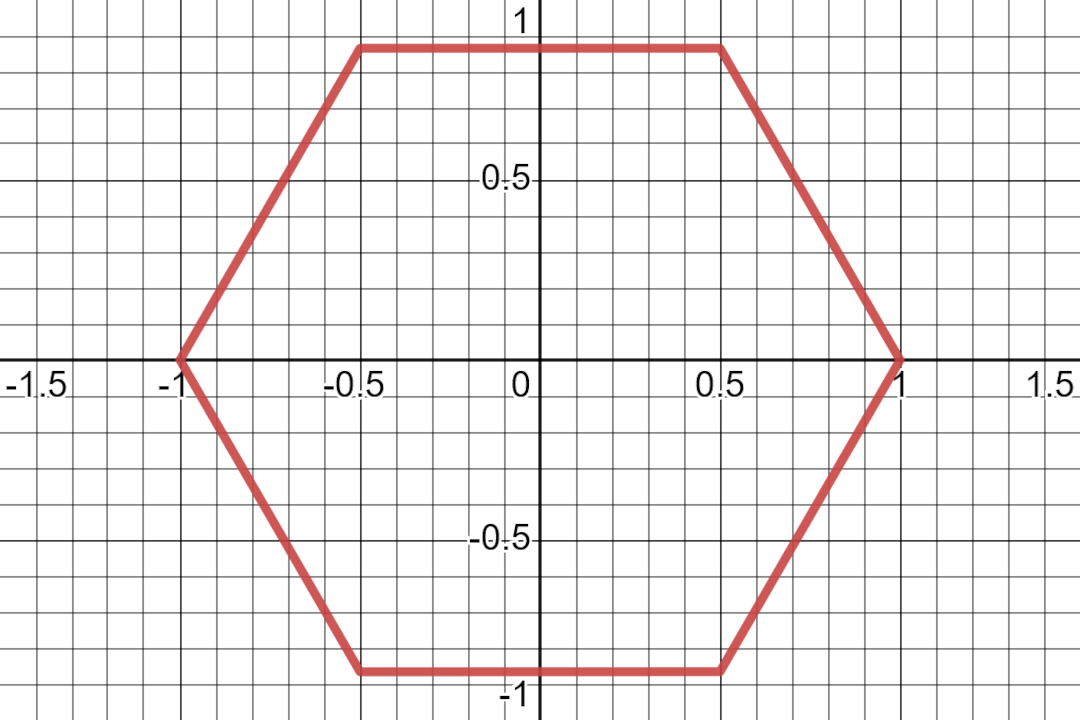
By using the distance equation defined above, we can calculate the length of each line of the hexagon3. This gives us a length of 1 for each line of the hexagon which means that the circumference is 6.
$$ 6 = C = 2 \pi r = 2 \pi (1) $$ $$ 3 = \pi $$
So next March, instead of just celebrating $\pi$-day on March 14th (3/14), feel free to celebrate $\pi$-month all through March. You just have to do the work of finding the appropriate metric for each day of the month.
I learned of the original article from this StackExchange post that summarizes the article. ↩︎
The StackExchange post gives the metric that has n-sided polygon as its circle. The article linked above hints that the “shape” that minimizes the value of $\pi$ is a hexagon. So we set $m = 6$ into the formula. Also, note that the $\pi$ in this formula is the regular $\pi$ since it’s derived using Euclidean trigonometry. ↩︎
If you miss textbook math problems where a crazy equation resolves into a neat simple answer, then you should calculate the distance with $x = \frac 1 2$ and $y = \frac {\sqrt 3} {2}$. ↩︎