Intuition for Cryptography

Locks are kinda amazing. A locked door is significantly harder to open than an unlocked door. But if you have the specific key, then suddenly a locked door is easy to open. The lock can make opening the door selectively difficult. It translates the presence or absence of a key into physical force. And this probably takes some really cool engineering. I am sure locks are complicated with all kinds of tumblers and pins interacting in ingenious ways. I don’t understand the mechanics but I still have useful intuitions around locks:

• The lock has to be used to provide any security.
• No lock is infinitely secure. With enough effort, any lock can be broken or opened.
• A lock doesn’t know me. It only knows the key. So anyone I give a key to can open the lock just as easily.

This intuition is useful. It doesn’t allow me to build new locks but it allows me to operate locks effectively.

Cryptography is how we make digital locks: it allows us to make an action selectively easier for some and harder for others. Instead of mechanical engineering, cryptography uses mathematics to build the locks. And just as we didn’t need to understand the internal mechanics of physical locks, we don’t need to understand the internal mathematics of cryptography to build intuition around it.

And similar to how the intuition for physical locks can be useful when operating locks, intuition for cryptographic systems can be useful when you need to use them. Different cryptographic systems are designed for different purposes and require different intuition so below I have grouped them by use-cases and further grouped the use cases by how many secrets they need.

No Secrets

Even when there are no secrets involved, cryptographic systems can be important. This is the case in hashing.

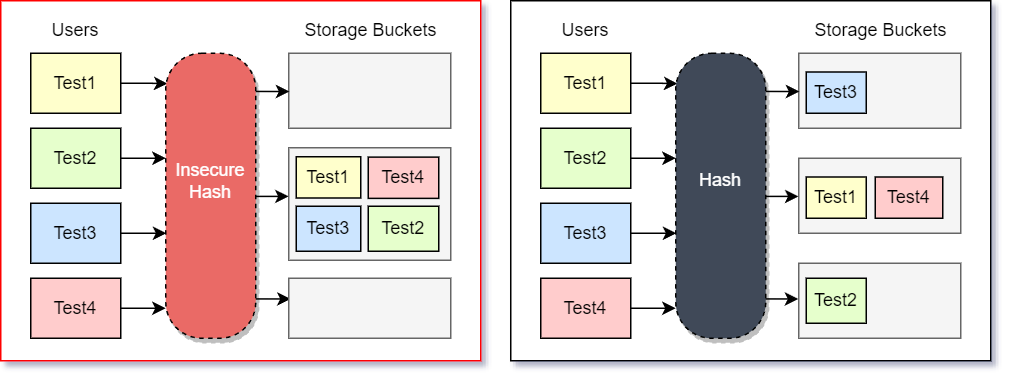
Hashing is used widely in software systems as it allows you to generate a shorter and mostly-unique identifier (called a hash) for a longer piece of data. These hashed values can be used in managing hashmaps, validating file integrity, or tracking data changes.

Non-cryptographic hashes are much faster but they don’t provide guarantees around being hard to reverse or to generate hash collisions. This can be a problem when they are used for validating file integrity (a malicious user can manipulate the file such that it still generates the same hash) or even when used for hashmaps that contain user-controlled keys (a malicious user can cause ALL keys to collide causing performance issues).

In these situations, you have to use a cryptographic hash. The only downside is that cryptographic hashes have to do more work and thus are slower.

We are ignoring the mathematical details but if you have to pick a secure hashing algorithm, libsodium defaults to blake2b. Don’t use md5 or sha1.

One Secret Key

Alright now we are in a world we are more familiar with. We have a key. What can we do with it?

Encryption

Going back to our example of physical locks: we can restrict access to something to only people that have keys. Our digital equivalent for restricting access using a key is encryption. Algorithms that encrypt and decrypt using the same key are called “symmetric encryption algorithms”.

While we are ignoring the mathematics of encryption algorithms, a complication does bubble up to the intuition level. It turns out that encrypting repeated data with the same encryption key is dangerous. A malicious user can collect these encrypted values and study them to find patterns. For example, in the image above you can still make out the figure in the encrypted image because similar blocks of color get encrypted to the same value. The block-by-block problem is solved by making each block’s encrypted value depend on all of the previous blocks but the larger message-by-message problem remains because the same full message will still encrypt to the same value.

To fix this, encryption algorithms will either ask you to pass in a random “initialization vector” or not-necessarily-random but unique “nonce” value. In either case, the encryption algorithm will use these inputs to alter the encryption process so that the same plaintext data will encrypt to different values even with the same key.

Data Integrity

With our secret key, locking/unlocking isn’t the only thing we can do. We can also check if anyone has touched our stuff.

Suppose we have some important file stored on a computer and before using the file we want to make sure that no one else has manipulated the file. Previously, we talked about how cryptographic hashes can be used for this.

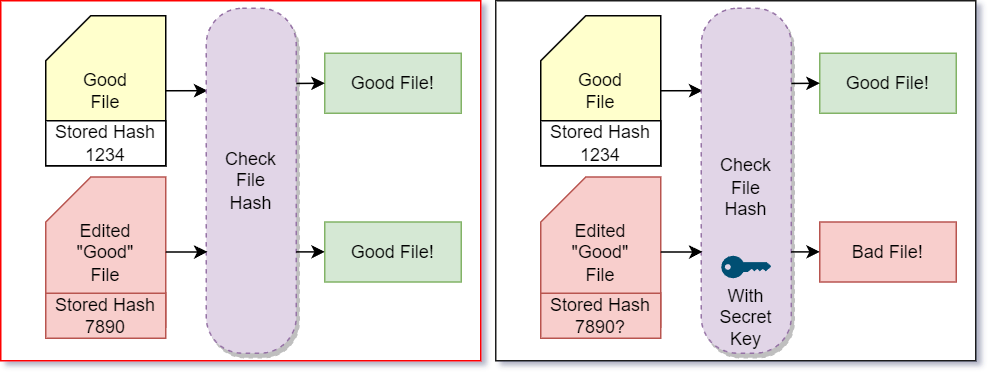
So we would hash the file anytime we changed the file. Then before using the file we would hash it again and make sure the hashes match. But where do we store the hash? If we put it next to the file, then the malicious user could also change the hash! This means we have to securely store the hash somewhere the malicious user can’t get to it. But if we had a place like that, we would have just put our file there!

We can solve this problem by generating a hash mixed in with our secret. This can be done using MACs (message authentication codes) which can take the input and your key and hash them together. If a malicious user alters your file, they won’t be able to generate a valid hash because they don’t know your key. Since the MAC can’t be spoofed, you can store the hash next to the file and still trust the authenticity and integrity of your file.

HMAC (with SHA256 or SHA512) is a common algorithm used to combine input data with a key to generate a hash. libsodium supports HMACs but defaults to using blake2b directly.

Authenticated Encryption

Now we have discussed encryption and integrity. It only seems reasonable to combine them! Before you decrypt a message, it would be nice to know that the encrypted message was not manipulated by a malicious user. That’s what authenticated encryption provides by generating a MAC in addition to encrypting the message.

Libraries that provide an easy-to-use interface for encryption will usually default to using authenticated encryption. That’s what libsodium’s crypto_secretbox_easy API does. That’s what age’s symmetric encryption algorithm uses. That’s what cryptography’s (python library) “unhazardous” encryption interface uses.

If your library is doing it right, hopefully, you don’t have to pick an encryption algorithm at all. But if you do: libsodium uses XSalsa20, age uses the related ChaCha20 algorithm and Python’s cryptography library uses AES (which is a little old school but still considered safe).

One Public Key, One Secret Key

Things are going great with my key. I can encrypt things. I can decrypt things. I can validate the integrity of my data. But I can only do this with my own private things. If someone wants to send me a secret message that only I can decrypt, I will have to give that person my secret key to encrypt a message. But if I do that, this person will be able to decrypt ALL my other data. How can I receive a secret message without sharing my secret key?

This is where public-key cryptography can help us. In such systems, encryption can be done with only a small part of the key. Only the decryption process needs access to the full key. So we take the part that is needed to encrypt and publish that as the “public” key for anyone to use to encrypt messages to us. We keep the rest of the key secret as our “private” key to handle the decryption part.

The way this works is that it uses a type of problem that is easy to create, hard to solve in general, and easy to solve when you have some specific information. You generate the “specific information” first and publish some general summary of that information as your public key. Then someone else encodes their message in a problem that should be easy to solve with the specific information.

A simple example of this might be puzzle-making. Suppose the “specific information” you have is an innate ability to solve crossword puzzles. So in your public key, you might say “I am really good at crossword puzzles”. Someone who wants to send you a message will have to spend some time to encode their message into a crossword puzzle and send it to you. And since you are really good at solving the crossword puzzle, you will find the encoded message before any other adversary does.

Of course, our crossword puzzle system is not great. Actual public-key cryptography systems use problems where problem generation is a lot easier and the general difficulty of solving the problem is much higher.

Asymmetric Encryption

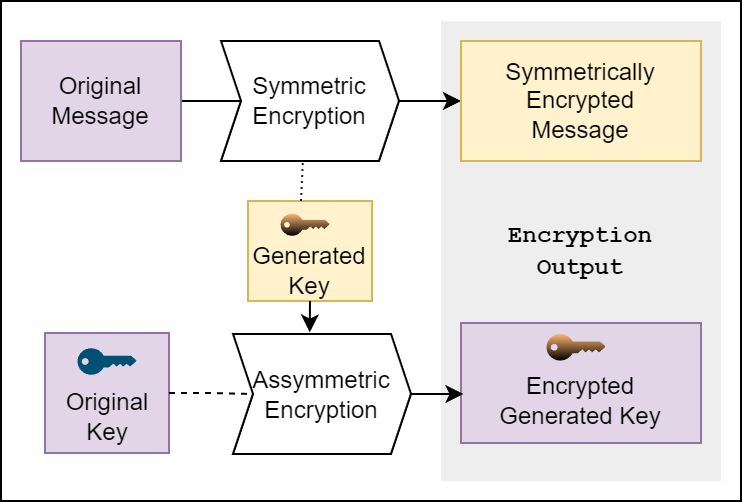
Public-key based encryption systems are also known as asymmetric encryption algorithms because they use different keys for encryption and decryption. One important thing to know about asymmetric encryption algorithms is that they are painfully slow. That’s the cost of the crazy magic that they do. Because of this, full messages are rarely encrypted using the public key. Instead, the message is first encrypted using the symmetric algorithm, and then the symmetric key is encrypted using the asymmetric algorithm. This way only a small key has to be encrypted/decrypted using the slower algorithm.

RSA and Elliptic Curve Cryptography (ECC) are the most widely used asymmetric encryption algorithms. Both rely on hard problems that are known to be easy for quantum computers. So if a large quantum computer ever gets built, all messages encrypted with RSA/ECC are at risk. To get ahead of this, the cryptographic community has been working towards post-quantum cryptography to find algorithms that don’t rely on problems that quantum computers can solve easily. While there is no final answer at the moment, I expect the “default” standard asymmetric algorithm to change within the next few years.

In the meanwhile, though, libsodium and age both use X25519 (which uses Elliptic Curve Cryptography) for asymmetric encryption¹.

Signing

Public-key cryptography can also be used for “hashing” messages where the private key is used to generate the hash and the public key is used to verify the hash. But now the hashes get a new meaning. In the symmetric case, we were using hashes to make sure that our data hadn’t changed. But now, by hashing data with our private key and sharing that hash, we certify to others that we have “signed” the message. Others can verify that the hashes match our public key and can be sure that the message came from us.

With this ability to digitally sign documents, we can verify claims by others as long as we can find their public key. And people can verify our claims, as long as they can find our public key.

Internet/TLS/SSL Certificates

Finding trustable public keys is the problem that the world of the internet had to solve. When you connect to a website, you want to know that no one else in the middle can snoop on your connection.

But the computer networks allow for many opportunities for others to snoop. So how can we start talking privately over this untrusted channel? We can’t exchange symmetric keys on this connection because the listener would also see the keys and be able to decrypt future messages². The website can send me its public key over this connection but I can’t trust it because the listener might hijack that message and switch out the public key for their public key.

So something outside this connection has to help me get or validate the public keys. That’s where Certificate Authorities (CA) come in. The job of the CA is to validate that the owner of a public key is also the owner of a given domain name. After the CA validates that³, it will sign the public key of the domain owner with the CA’s own key.

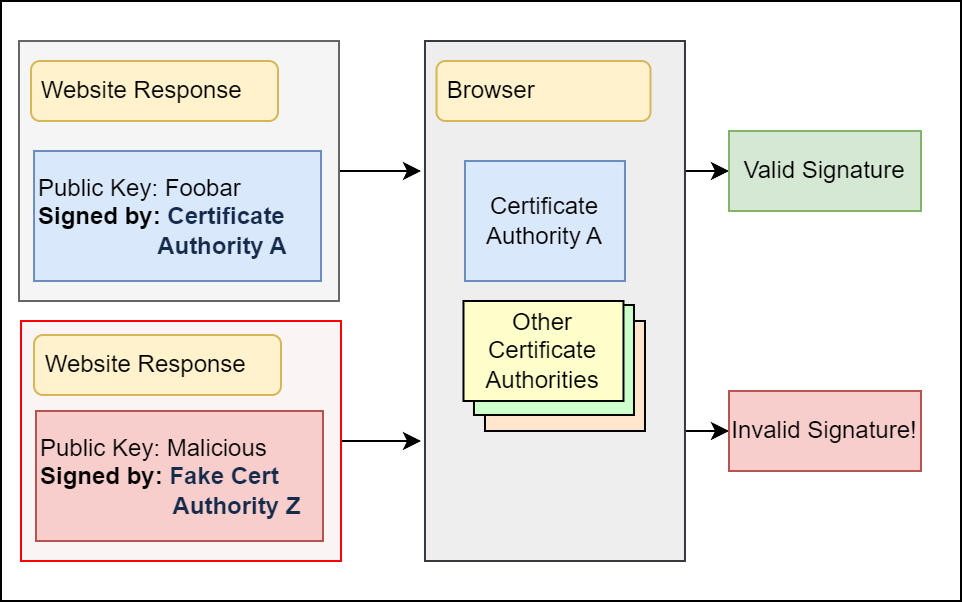
The website owner has to do this step before they talk to me. When they start talking to me, the website will first send the signed public key (also known as a certificate). My browser has a list of CAs that they trust (and the public keys of those CAs). The browser will use the public key of the CA that signed this certificate to validate the signature. If the signature matches, then the browser trusts the public key of the website. Once this trust is established, asymmetric encryption can allow for a new symmetric key to be shared which will allow for the rest of the communication on the channel to be securely encrypted!

Conclusions

Cryptography is kinda amazing. It allows us to solve problems by translating them into mathematical problems that are hard to solve for most people and are selectively easy to solve with specific information. Hashing without secrets allows us to validate the integrity of data. Hashing with a secret allows us to validate the integrity of data without having to safely store the hash. Encryption with symmetric keys allows us to lock away our data so only we can look at it.

Asymmetric encryption changes the game, allowing us to encrypt a message for someone without having to share a secret with them. Generating a hash with a private key also allows us to digitally sign a message so that everyone else can verify our signature. Asymmetric encryption is limited by the problem of acquiring trustable public keys. For the internet, this problem is solved by browsers trusting Certificate Authorities to vet domain owners and signing their keys after the vetting.