Infinity is weird. It’s amazing that we have the mathematical machinery to work with infinite systems at all. For example, we can calculate sums of infinite numbers, we can evaluate functions at infinity and we can work with probabilities even when there are infinite possibilities. But there are limits to this machinery.
At some point, the mathematical system must be applied to the finite world and we have to understand how the behavior of the system changes when facing finiteness.
Infinite Hotels
We can take the “infinite hotel” as our first example. Imagine we are running a hotel with infinite rooms and all rooms are occupied. When a new guest arrives, we can still accommodate them by asking each guest to move over to the next room. It’s weird but this works. All guests will get a room.
If we assign each room a number, then all we are doing is assigning each guest to the n+1 room. Since n+1 is always a valid hotel room, we will have a room for all the guests.
| Original Room | New Room |
|---|---|
| 1 | 2 |
| 2 | 3 |
| 3 | 4 |
| … | … |
n | n + 1 |
| … | … |
But when we try the same thing with a finite hotel,
we run into a problem. The guest in the last room is asked to move to the
“next” room but we are at the end and there is no other room left. n+1 is not always valid in a finite world.
This is the problem infinite systems run into when they are approximated by finite systems. Infinite systems don’t have to handle behavior at the edges but finite systems do.
Infinite Physical Models
In Physics, a lot of systems are modeled using partial differential equations which allow you to relate how the system is changing in time and changing in space.
For example, the wave equation says that a wave accelerates in time proportionally to its “acceleration” in space. This equation describes the behavior of a wide variety of things like guitar strings, drum skins, ripples in water, and radio signals.
The wave equation needs more data to give you an exact solution though. It needs the starting state of the system and it needs to know the boundary of the system. We can imagine a system that sends off new waves every second into infinite space so the boundary of the system is infinity.
This is what such a system will look like:
That makes the behavior of the waves nice and easy to see. The wave starts in the center and propagates outwards at a constant rate weakening slightly as it does so.
However, if we give a finite boundary condition to the wave equation, we see a much different result.
As the waves approach the boundaries, they are reflected back and the behavior of the system shifts dramatically. Instead of clear isolated waves, we are left with multiple interacting waves with some spots that may never get the original signal without interference.
Partial differential equations are defined by their behavior at the boundaries and changing between infinite and finite boundary conditions fundamentally alters their behavior. The finite boundaries introduce a lot of complexity at the edges, which the infinite systems get to ignore.
Ponzi Schemes
This is the disappointing problem with Ponzi schemes too. In a Ponzi scheme, you keep taking on new investor money to pay the old investors amazing interest/dividends. Eventually, people figure out that you aren’t actually growing the investments in any sustainable manner, and they all ask for their money back since they don’t want to be left holding the proverbial bag. And because of that, the scheme falls apart.
But running for the doors is only rational in a finite world. In an infinite world, with infinite investors, a Ponzi scheme is a great idea! There are always infinite remaining investors so you can always pass the bag to the next person! Since no one has to worry about the end no one has to worry about losing their investment. The Ponzi scheme will continue to make everyone money, forever!
So Infinite-Ponzi-Schemes, great. Finite-Ponzi-Schemes not so much.
Exponential Growth & Resource Limitation
Real-life systems demonstrate exponential growth pretty often. So when we study these systems, we usually start by modeling them as systems that will keep evolving exponentially. But this requires the system to have infinite resources and most of the time the resources are finite1. And, hitting this finiteness can transform the system dramatically.
Sigmoid Curve
A sigmoid curve is a function that shows fast growth initially and at some point slows down and tapers off to an asymptote.
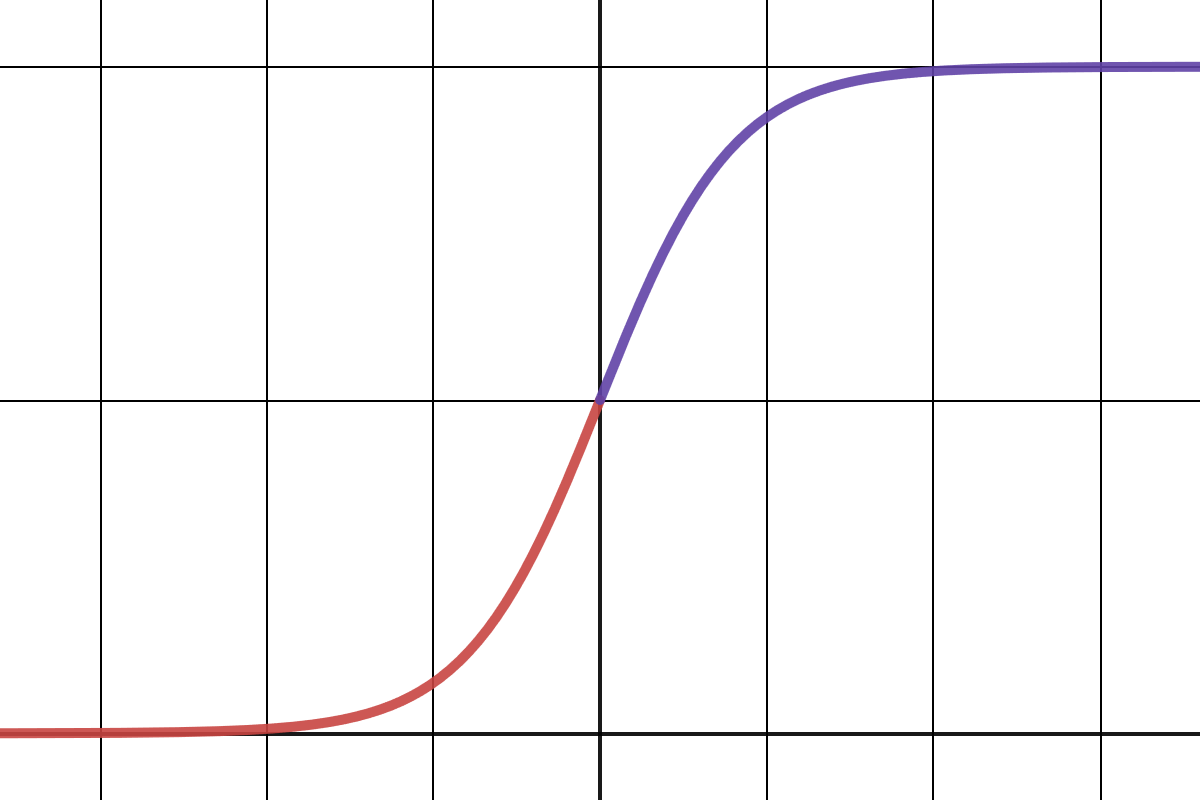
Business
In the world of startups, businesses are looking for exponential growth and plan their strategy, hiring, and finances around that. And the sigmoid is what they have to worry about. Even if the business finds success and grows exponentially at first, it is easy for the company to run into the limits of the market. This can happen on the demand side (limited customers, competitors adapting) or the supply side (limited hiring pool, finite sources of raw materials). When that happens, the exponential growth turns into the saturated asymptote seen above.
For many startups that only plan for exponential growth, slowed-down growth can easily be enough to end the business.
Chemistry
In chemistry, you can have a reaction where X and Y mix to produce chemical Z. Some chemical reactions can benefit from a catalyst such that if a catalyst C is present, then the reaction will proceed much faster. The generation of Z doesn’t require the catalyst, it just benefits from it.
There are some reactions where the output chemical Z is also a catalyst for the reaction. So as more chemical Z is produced, the reaction becomes faster and produces even more of Z. This is called autocatalysis and shows the sigmoidal behavior discussed above. The reaction speed grows exponentially till reactants A or B start running out and slowing down the reaction.
This behavior of autocatalysts results in the Briggs-Rauscher Reaction which is a cyclical reaction that is easy to visualize: the color of the solution rapidly alternates between blue, clear, and yellow. This is caused by the autocatalytic process rapidly generating a side product (iodide) in such high quantities that it disrupts the reaction. This allows for a much slower process to win out but this process ends up clearing out the iodide that was disrupting the original process. As a result, the point of equilibrium constantly shifts back and forth between the two reactions.
In an infinite system with infinite reactants, an autocatalyst will get faster and faster generating more and more of itself. In a finite world though, it can result in a cyclic reaction where the quantity of the autocatalyst can go down.
Martingale Betting System
Gamblers love coming up with foolproof betting strategies. The Martingale is one such system.
Imagine you are playing a game where a coin is tossed every round. If it comes up heads, you win double your bet. If it comes up tails, you lose your bet. In a Martingale system, anytime you lose, you just bet twice as much in the next round. This way, whenever you win, you make up for all losses. Since you are bound to win eventually, you will come out ahead!
For illustration, imagine you start with a bet of $1. You lose the first three coin tosses and then win on the fourth.
| Coin | Bet | Result | Total |
|---|---|---|---|
| Tails | $1 | -$1 | -$1 |
| Tails | $2 | -$2 | -$3 |
| Tails | $4 | -$4 | -$7 |
| Heads | $8 | +$16 | +$9 |
Because you kept doubling your bet, you eventually came out ahead with $9. So what’s the problem here?
The problem is that your losses keep growing exponentially. When you run into a bad streak, it takes very few rounds to ruin you completely! Once you are out of money, you can’t make any future bets and you are out of the game.
Because exponential growth is so fast, your bet size grows to $1,000 after a bad streak of 9 rounds. It grows to a million in 18 rounds and a billion in 28 rounds.
So to protect our initial $1 bet, we have to be willing to back up our bets with larger and larger pools of money. With an infinite bankroll, you are guaranteed to come out ahead. With a finite bankroll though, you are taking an actual risk.
When systems are being used to make predictions or decisions, you have to know the assumptions of the system and how the system fails when the assumptions are violated. It’s fine to use infinite systems–they make a lot of calculations easier precisely because they can ignore the ugliness at the edges. You just have to know the scale at which you will hit finiteness and how the system will change when it does.
A fun exception is the expansion of the universe. One possibility for the future of our universe is the Big Rip in which the universe keeps expanding at a faster and faster rate to the point that it starts ripping apart atoms. Since the expansion is intrinsic to the universe itself, there is no resource to run out of. ↩︎