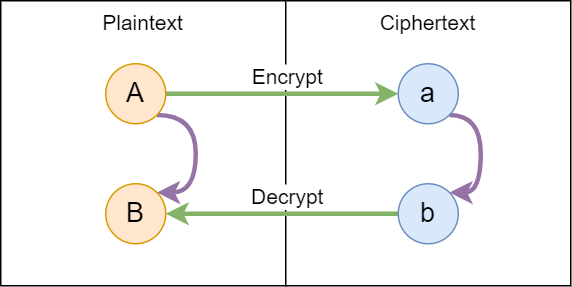
Homomorphic encryption is a form of encryption that allows you to do computations on encrypted
data! The image above provides a simple model for this. Suppose changing a capital letter (A)
to its lowercase version (a) is the encryption algorithm. In this system, we can do computation
on the encrypted letter. Suppose the computation is to increment the letter (a -> b). If we decrypt the new
value (b -> B), it will be equal to doing the computation directly on the original plaintext (A -> B).
Background
My first exposure to homomorphic encryption was reading a blog post by Bruce Schneier. He highlights that normally we want encryption algorithms to “look” random:
Assume you have a plaintext P, and you encrypt it with AES to get a corresponding ciphertext C. If you multiply that ciphertext by 2, and then decrypt 2C, you get random gibberish instead of P. If you got something else, like 2P, that would imply some pretty strong nonrandomness properties of [the encryption system]
However, RSA (and some other asymmetric algorithms) have this exact “homomorphic” property! This is the reason that asymmetric algorithms are expected to have much longer keys because they are more structured than symmetric algorithms. While RSA maintains the homomorphic property for multiplication, other algorithms maintain this property for addition. The Wikipedia article highlights more systems that maintain other homomorphic properties, including various “Fully Homomorphic” systems that can handle all computations.
Image Analysis
While looking around for applications for homomorphic encryption, I found two interesting papers applying homomorphic encryption to graphics applications. Interestingly both used the Paillier cryptosystem which is a partial homomorphic system that only supports addition.
Ziad et al implemented a bunch of image algorithms on encrypted data in “CryptoImg: Privacy Preserving Processing Over Encrypted Images”.
Mazza et al implemented a limited version of ray-tracing in “Homomorphic-Encrypted Volume Rendering”. While this raytracing system can’t support reflections, it can be used to render X-rays/CT scans without leaking patient data. This can be done because a ray can “accumulate” all the material it intersects with using only addition.
Available Libraries/Frameworks
An industry group of IBM/Microsoft and others maintains a list of libraries/frameworks that are available. awesome-he on GitHub also provides a list of libraries but it lists things alphabetically which feels less useful.
Based on my searching, it seem that Microsoft’s SEAL library is pretty popular. Microsoft also provides a higher level interface called EVA. However, EVA requires building from source while Pyfhel is a python interface for SEAL that is already published on PyPi. So for getting up and running quickly, I chose to use Pyfhel.
My testing


Microsoft’s EVA repo has an example of edge detection implemented over an encrypted image. I wanted to reimplement this in a true client/server model to have separation between process that knows the secret key and the process that doesn’t. I published my code at azeemba/homomorphic-encryption-testing.
I first implemented the edge detection algorithm (which honestly was very cool on its own). After parallelizing the algorithm, I was able to analyze a 512x512 image in 0.2 seconds.
Then I implemented a HTTP server and a client. The client first encrypts the image and sends it to the server. The server then applies the edge detection algorithm over the encrypted image and sends the result back. Then the client decrypts the results.
I parallelized the encryption process because that was by far the slowest step. Encrypting a 512x512 image on 12 cores took more than 800 seconds (~14 mins)! However, since homomorphic encryption increases the size of the ciphertext by so much, the encrypted image was causing the processes to run out of memory.
Part of the problem was the client/server relationship causes the data to be duplicated in both. I did improve this by implementing streaming of responses and this was enough to fully complete the request/response for a 256x256 image. Processing of a 256x256 image took:
- Encryption: 200 seconds (~3 mins)
- Streaming edge detection + decryption: 60 seconds
- Max Memory: 12GB
So an edge detection algorithm that was taking 200 ms blew up to an end-to-end time of 260 seconds when using homomorphic encryption. This is an increase of 3 orders of magnitude of runtime! I think the increase in memory usage is the biggest problem though since current computing world is more bound by RAM than by CPU.
Conclusions
While the blog post mentioned earlier is from 2009, I think the observation of the practical limitations of FHE still stands true. In addition to impracticalities of building a full boolean circuit for any program, I think there are limitations even in the use case of doing pure data processing. I think as long as the encryption process is so expensive, there are limited justifications for doing that heavy work on the client side only to delegate something less expensive to another untrusted system.
Maybe a use case is where an algorithm owner doesn’t want to share their algorithm with others and data owners don’t want to share their data with the algorithm-owner. The data owners can’t run the algorithms themselves so they encrypt their data and send that over to the algorithm owner. This could work if this interaction doesn’t have to be realtime but does feel like a very specific/unlikely use case.