Degenerate Matter: How Reality Deals With Uncertainty

Uncertainty Principle

Quantum Mechanics is wild. It makes the universe feels wobbly. Or, rather, it makes me feel wobbly about the universe.

One of the sources of this wobbliness is the uncertainty principle. It is often incorrectly quoted as “you can’t know the position and momentum of a particle simultaneously”. This effect does exist: when you measure one property of a quantum system you do irreversibly change the system. This is the other source of wobbliness in quantum mechanics and is called the measurement problem. This is more closely related to Schrodinger’s cat and questions about the “interpretations” of quantum mechanics.

So if this is not the uncertainty principle, then what is?

Let’s start with the probabilistic nature of Quantum Mechanics. A particle doesn’t have an exact location. It has some probability of having one position and some other probability of having another position (the collection of all these probabilities is called the probability distribution). Note that these probabilities are fundamental: the particle behaves as if it is occupying all of those positions. This is the famous wave-particle duality.

So if we were working with these quantum particles, how would that impact us? One change would be that instead of controlling the particle’s exact starting position and momentum, we could only control the probability distribution for those values.

This doesn’t seem too bad! Can’t we just set the particle to have probability close to 1 at the location we want and 0 everywhere else? To keep the probability distribution smooth, we can spread out the high probability over a narrow region as seen below. Then we can just kinda ignore all the probability crap since we basically have the particle locked in the exact position we need to the precision we want.

However, as we start running this experiment we notice that the particle’s momentum is taking wild swings. As the position’s probability distribution is made narrower, the variance in the momentum seems to increase.

The graph below shows the actual probability distribution of a particle in a one dimensional box. As the box is made smaller, the potential range for where the particle can exist is made narrower. However, as the box is made narrower, the momentum probability distribution widens so that it takes on a wider range.

Note that this is not a limitation of measurement. In quantum mechanics, the position distribution and the momentum distribution are fundamentally linked. If you choose a position distribution, you are automatically choosing the momentum distribution. The two are linked in a way that if one distribution becomes too narrow, then the other distribution will get less narrow.

This is the uncertainty principle. If a particle’s position is distributed in a more narrow range of values, then its momentum is distributed in a larger range of values. And if the momentum of a particle was restricted in a narrow range, then its position distribution would take on a wider range of values¹.

Knowing this relationship, we can ask an interesting question: what happens at the extremes? What happens when the position distribution is made as narrow as possible? What happens when the momentum distribution is made as narrow as possible?

Fermions and Neutron Stars

In our day-to-day world, we know that two different things can’t exist in the same place. Video games mess this up occasionally and show two things clipping through each other and occupying the same space. These glitches stand out to us because they violate our expectations about how the world works.

At the quantum level, many of the well-known particles (protons, neutrons, electrons) follow a similar rule known as the Pauli exclusion principle. The specific rule is that two particles can’t occupy the same quantum state in the system. The quantum state is kinda like the position because the quantum state controls the particle’s probability distribution. Also, the availability of quantum states matches our expectation of physical space in general: when there is more physical space available in a system, there are more quantum states available and where there is less physical space available, there are fewer quantum states available.

So if we squint, then the Pauli Exclusion Principle matches our day-to-day intuition about objects not overlapping.

This is good news for us because it means that if we have a macroscopic object made up of these particles, then we can restrict their position to narrower ranges by simply compressing the macroscopic object. Since the particles won’t overlap, each particle individually will be restricted to a narrower position range.

So now we have macroscopic objects that we want to compress. What’s the best way to generate maximal compression? For that, we have to look to gravity and the stars.

Gravity is persistent. So when there is a big ball of matter, gravity constantly will try to pull things closer and try to make the ball smaller in size. The ball will get smaller till something can stop it. As the ball gets smaller, enough pressure builds up in the core of the ball that it triggers nuclear fusion. This is how a ball turns into a star.

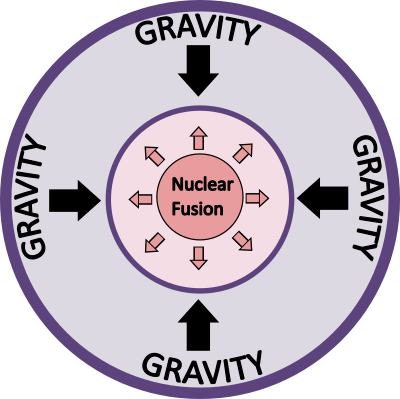
The star remains stable as long as the pressure from gravity remains in balance with the pressure generated by the nuclear fusion. Eventually though, a star will run out of juice and won’t be able to continue the nuclear fusion. At this point, gravity takes over and the star implodes and collapses in on itself. The implosion releases so much energy that the exterior of the star explodes away creating a supernova².

Since there is nothing fighting gravity, the star gets smaller and smaller. The gravity of the collapsing star generates so much pressure that all the protons and electrons inside the star combine to make neutrons. Eventually, it gets so small, that the Pauli exclusion principle becomes important and stops the star from collapsing further!

How does this work? Well the exact way requires a lot of math, so we will take a hand-wavy simplified approach. As the star is shrinking, the neutrons get more and more tightly packed as shown in the video below. This means that the neutron has to occupy a smaller amount of space because they can’t overlap. Because of the uncertainty principle, when a particle is locked in a smaller space then its momentum has to take on values in a wider range. This increase in momentum across all the neutrons creates an outward pressure that starts resisting gravity³. This outward pressure is known as degeneracy pressure and that’s what keeps the neutron star from collapsing further and becoming a black hole.

So the uncertainty principle and Pauli exclusion principle are what lead to neutron stars! And Neutron stars are incredible. They are one of the densest objects in the universe. They are so dense that if our sun was a neutron star it would be the size of a small town! The smaller radius of the neutron star also leads to crazy rotational speeds. This effect is similar to how figure skaters spin faster when they fold in their arms, only on an astronomical scale. Some neutron stars do a full rotation every few milliseconds!

Most neutron stars rotate so much that they create lots of electromagnetic energy. This electromagnetic energy is shot out like a laser beam from the magnetic poles of the star (though we don’t know the exact mechanism of how). So from Earth, these stars look like a lighthouse as the star’s beam of energy sweeps across the universe. These stars are knowns as pulsars and their regular lighthouse-like flashing allows us to study astrophysics by using them as clocks and landmarks.

It’s cool to think that this all only works because neutrons don’t like sharing space and locking them in smaller spaces makes them fidgety.

Bosons and Superfluids

Particles that follow the Pauli exclusion principle are known as fermions. The particles that don’t are known as bosons. This is not their actual definition but it’s good enough for us.

One example of a common boson “particle” is a photon (i.e light) but atoms like Helium are also bosons. Multiple bosons in a system can occupy the same energy state⁴. Since lower energy means lower momentum, we can use bosons to see what happens when the momentum probability distribution is made narrower (between 0 and the momentum allowed by the energy level).

Lowering the energy of a system is basically the same as cooling a system. However, our regular cooling solutions like air conditioning will not be enough here because we want to reach crazy low temperatures close to absolute zero (-273 C). For this, we need fancier things like laser cooling which just sounds amazing and evaporative cooling which sounds hilariously normal but is just as complex.

So what actually happens when all bosons in a system occupy the lowest energy state. Here is a video by QuantumMadeSimple that explains:

In case you didn’t feel like watching the video:

• The system is cooled till all the particles are in the lowest energy state
• Each particle’s momentum has the lowest possible value so each particle’s position probability distribution is very wide
• The particle’s position distribution is so wide that all the particles start interfering with each other
• The interference results in the whole system behaving like one macroscopic quantum wave

When Helium is cooled like this, it turns into a superfluid which means it behaves like a fluid with 0 viscosity/resistance. It is known to creep up the side of the containers and escape, escape through microscopic pores and also create frictionless fountains. The macroscopic quantum nature of the superfluid is most visible with rotation.

In quantum mechanics, a lot of measurable quantities are not continuous–only specific discrete values are allowed. The same applies for angular momentum/rate of rotation which means that a quantum object can only rotate at specific rates.

This discrete behavior can be seen in the diagram below which is based on data from an experiment from 1980⁵. In this experiment, a superfluid is put inside a rotating container. The container’s rotation speed is changed and the superfluid’s rotation speed is measured (indirectly). If this experiment is done with a regular fluid, we would see the fluid rotate at the same rate as the container. But since superfluids behave like quantum objects we see the discrete jumps in the data. As the rotation rate of the container is increased, for a while the fluid doesn’t rotate at all since the closest allowed value for the rotation is 0. Then as the container is rotated faster, the fluid jumps to the next allowed rotation rate. In this way, the superfluid behaves like a macroscopic quantum object.

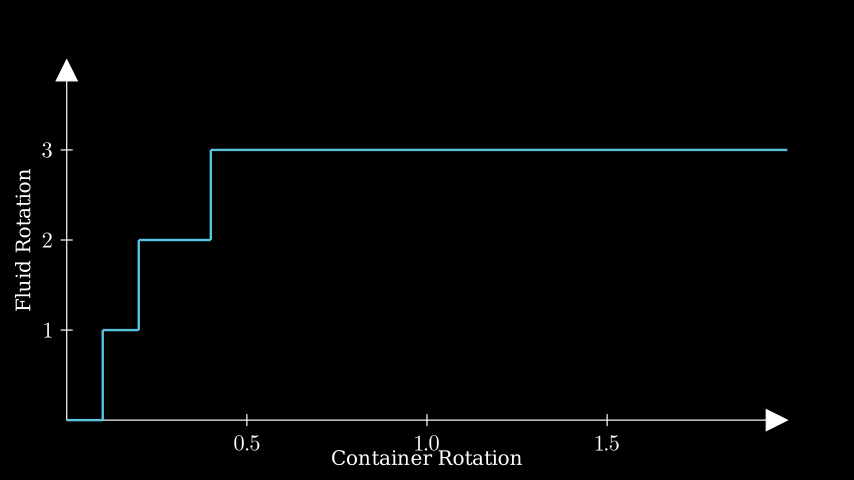
So because bosons like to share state and because they spread out when they slow down, we get to see quantum effects in macroscopic fluids!

Conclusions

We made a lot of simplifications but the picture we painted is roughly accurate. Quantum mechanics impacts macroscopic things. This is true even without going to the extremes (computer chips are a common example of something that only works because of quantum mechanics). However, when we do go to the extremes, the uncertainty principle results in some really cool phenomena.

Fermions resist sharing state which allows for their position to be more restricted in neutron stars, and this results in a degeneracy pressure that stops the star from collapsing. So neutron stars exist only because of the uncertainty principle and the Pauli exclusion principle.

Bosons are okay sharing state so a group of them can be cooled down to their lowest allowed energy state which results in the group to behave like a macroscopic quantum object. So because of the uncertainty principle, we can see a macroscopic manifestation of other parts of quantum mechanics.